转载

OpenAI研究深度线性网络中的非线性计算

我们已经证明，使用浮点运算实现的深度线性网络实际上不是线性的，可以执行非线性计算。我们使用进化策略在利用此特性的线性网络中找到参数，让我们解决重要的问题。

神经网络由线性层堆栈组成，后跟非线性层，如 tanh 或整流线性单元。如果没有非线性，连续的线性层在理论上将在数学上等同于单个线性层。因此，令人惊讶的是，浮点运算的非线性足以产生可训练的深度网络。

背景

计算机使用的数字不是完美的数学对象，而是使用有限位数的近似表示。计算机通常使用浮点数来表示数学对象。每个浮点数由分数和指数的组合表示。在 IEEE 的 float32 标准中，23 位用于小数，8 位用于指数，1 位用于符号。

由于这些约定和使用的二进制格式，最小的正常非零数（二进制）是 1.0..0 x 2^-126，我们将其称为 min 。但是，下一个可表示的数字是 1.0..01 x 2^-126，我们可以将其写为 min + 0.0..01 x 2^-126。很明显，第二个数字之间的差距比 0 和最小值之间的差距小 2^20 倍。在 float32 中，当数字小于可表示的最小数字时，它们会被映射为零。由于这种“下溢”，在零附近所有涉及浮点数的计算都变得非线性。

这些限制的一个例外是 denormal numbers，它可以在某些计算硬件上禁用。虽然 GPU 和 cuBLAS 默认启用了非正规化，但 TensorFlow 构建其所有基元时都关闭了非正规化（设置了标志 ftz=true ）。这意味着任何用 TensorFlow 编写的非矩阵乘法运算都有一个隐含的非线性跟随它（假设计算规模接近 1e-38）。

因此，虽然通常任何“数学”数字与其正常浮点表示之间的差异很小，但在零附近存在很大差距并且近似误差可能非常显着。

这可能会导致一些奇怪的效果，即熟悉的数学规则不再适用。

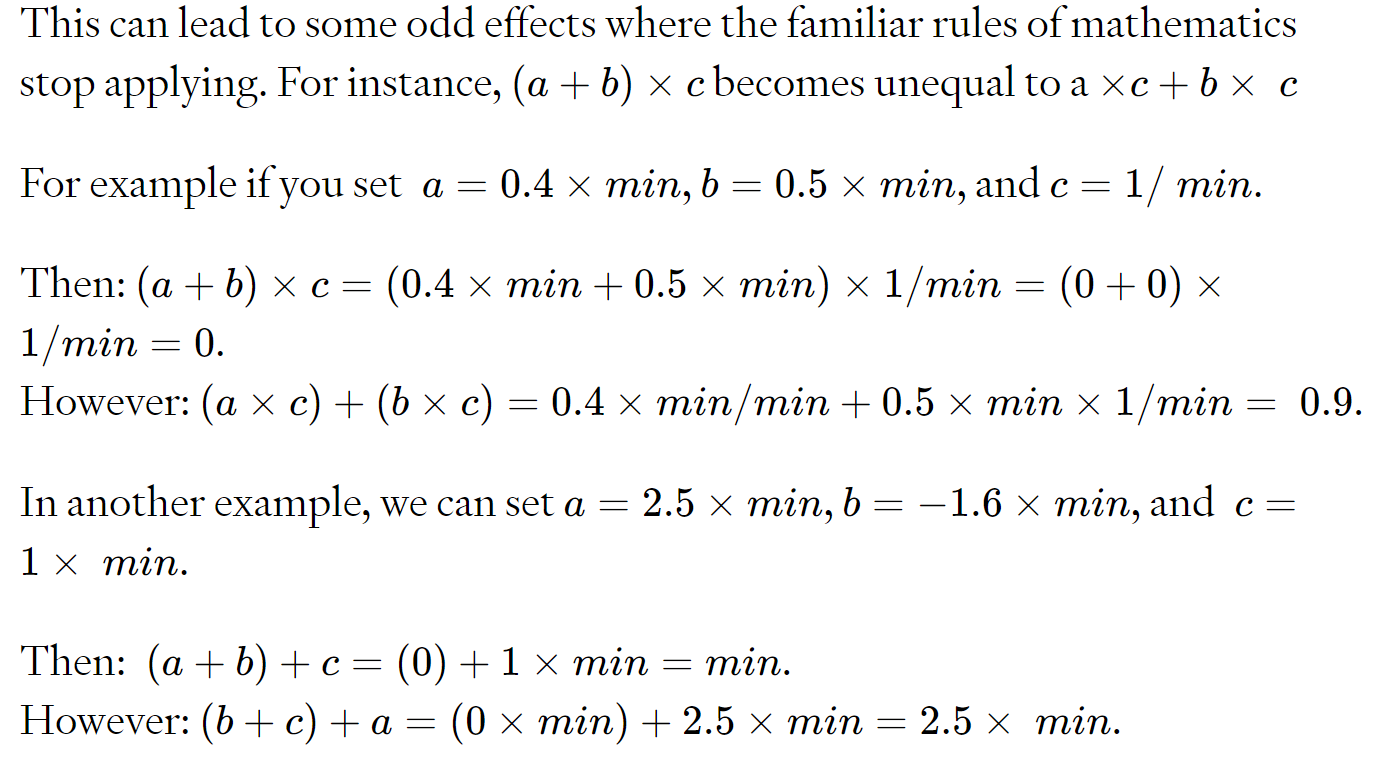
在这个最小尺度上，基本的加法运算已经变成非线性的了！

利用进化策略利用非线性

我们想知道这种固有的非线性是否可以用作计算非线性，因为这会让深度线性网络执行非线性计算。挑战在于，现代微分库对这些最小规模的非线性视而不见。因此，很难或不可能训练神经网络通过反向传播利用它们。

我们可以使用进化策略（ES）无需依赖符号微分即可估计梯度。使用 ES，我们确实可以利用 float32 的近零行为作为计算非线性。当在 MNIST 上训练时，通过反向传播训练的深度线性网络达到 94% 的训练精度和 92% 的测试精度。相比之下，相同的线性网络在使用 ES 进行训练并确保激活足够小以处于 float32 的非线性范围内时，可以实现 >99% 的训练和 96.7% 的测试精度。训练性能的提高是由于 ES 利用了 float32 表示中的非线性。这些强大的非线性允许任何层生成新颖的特征，这些特征是低层特征的非线性组合。这是网络结构：

x = tf.placeholder(dtype=tf.float32, shape=[batch_size,784])
y = tf.placeholder(dtype=tf.float32, shape=[batch_size,10])

w1 = tf.Variable(np.random.normal(scale=np.sqrt(2./784),size=[784,512]).astype(np.float32))
b1 = tf.Variable(np.zeros(512,dtype=np.float32))
w2 = tf.Variable(np.random.normal(scale=np.sqrt(2./512),size=[512,512]).astype(np.float32))
b2 = tf.Variable(np.zeros(512,dtype=np.float32))
w3 = tf.Variable(np.random.normal(scale=np.sqrt(2./512),size=[512,10]).astype(np.float32))
b3 = tf.Variable(np.zeros(10,dtype=np.float32))

params = [w1,b1,w2,b2,w3,b3]
nr_params = sum([np.prod(p.get_shape().as_list()) for p in params])
scaling = 2**125

def get_logits(par):
    h1 = tf.nn.bias_add(tf.matmul(x , par[0]), par[1]) / scaling
    h2 = tf.nn.bias_add(tf.matmul(h1, par[2]) , par[3] / scaling)   
    o =   tf.nn.bias_add(tf.matmul(h2, par[4]), par[5]/ scaling)*scaling
    return o

无效的

除了 MNIST，我们认为其他有趣的实验可以将这项工作扩展到递归神经网络，或者利用非线性计算来改进复杂的机器学习任务，如语言建模和翻译。我们很高兴与我们的研究人员一起探索这种能力。

OpenAI研究

OpenAI研究深度线性网络中的非线性计算

背景

利用进化策略利用非线性

相关文章

本文目录

标签

近期评论

OpenAI研究 深度线性网络中的非线性计算

背景

利用进化策略利用非线性

相关文章

本文目录

标签

近期评论

OpenAI研究深度线性网络中的非线性计算